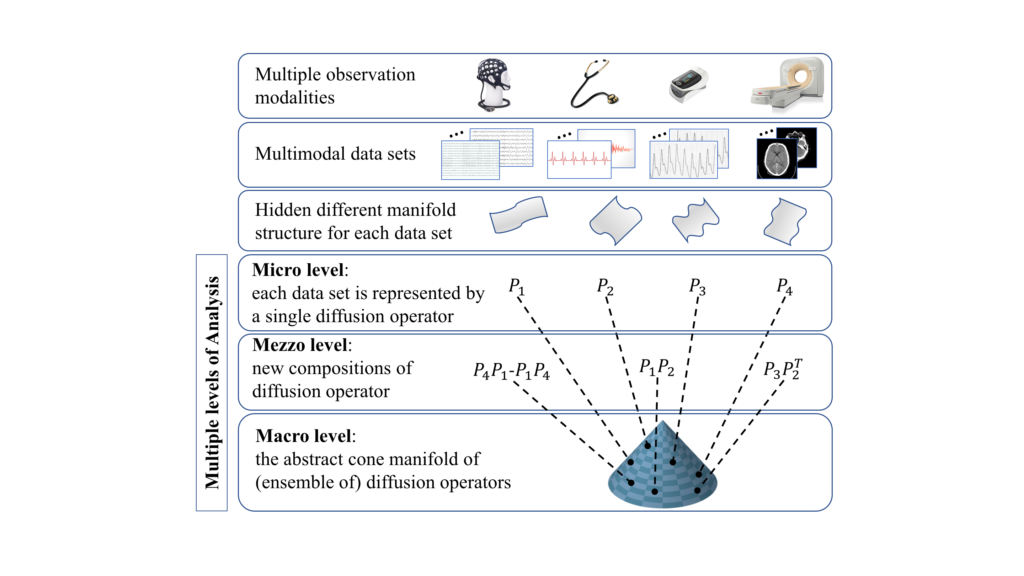
Nowadays, extensive collection and storage of massive data sets have become a routine in multiple disciplines and in everyday life. These large amounts of intricate data often make data samples arithmetic and basic comparisons problematic, raising new challenges to traditional data analysis objectives such as filtering and prediction. Furthermore, the availability of such data constantly pushes the boundaries of data analysis to new emerging domains, ranging from neuronal and social network analysis to multimodal sensor fusion. The combination of evolved data and new domains drives a fundamental change in the field of data analysis. Indeed, many classical model-based techniques have become obsolete since their models do not embody the richness of the collected data. Today, one notable avenue of research is the development of nonlinear techniques that transition from data to creating representations, without deriving models in closed-form. The vast majority of such existing data-driven methods operate directly on the data, a hard task by itself when the data are large and elaborated. The goal of this research is to develop a fundamentally new methodology for high dimensional data analysis with diffusion operators, making use of recent transformative results in manifold and geometry learning. More concretely, shifting the focus from processing the data samples themselves and considering instead structured data through the lens of diffusion operators introduce new powerful “handles” to data, capturing their complexity efficiently. We study the basic theory behind this nonlinear analysis, develop new operators for this purpose, and devise efficient data-driven algorithms. In addition, we explore how our approach can be leveraged for devising efficient solutions to a broad range of open real-world data analysis problems, involving intrinsic representations, sensor fusion, time-series analysis, network connectivity inference, and domain adaptation.